Lógica Matemática

La lógica matemática es una parte de la lógica y las
matemáticas, que consiste en el estudio matemático de la lógica y en la
aplicación de este estudio a otras áreas de las matemáticas. La lógica
matemática tiene estrechas conexiones con la ciencias de la computación y la
lógica filosófica.
La lógica matemática estudia los sistemas formales en
relación con el modo en el que codifican nociones intuitivas de objetos
matemáticos como conjuntos, números, demostraciones y computación.
La lógica matemática suele dividirse en cuatro subcampos:
teoría de modelos, teoría de la demostración, teoría de conjuntos y teoría de
la recursión. La investigación en lógica matemática ha jugado un papel
fundamental en el estudio de los fundamentos de las matemáticas. Actualmente se
usan indiferentemente como sinónimos las expresiones: lógica simbólica( o
logística), lógica matemática, lógica teorética y lógica formal.
La lógica matemática no es la''lógica de las
matemática'' sino la''matemática de la lógica''. Incluye aquellas partes de la
lógica que pueden ser modeladas y estudiadas matemáticamente

La lógica se ocupa del razonamiento a partir de premisas,
que dan la pauta para el proceso deductivo e inductivo. Inferir es unir ideas
para llegar a la conclusión verdadera a partir de preposiciones. El
razonamiento lógico es una operación lógica que partiendo de juicios, se deriva
la validez, posibilidad o falsedad de otro juicio. Existen varios tipos de
razonamiento lógico, por ejemplo: razonamiento deductivo, razonamiento
inductivo, etc. Razonamiento deductivo parte de lo general a lo particular.
TABLAS DE VERDAD
Tablas de verdad o tabla de valores de verdad, es una tabla
que muestra el valor de verdad de una proposición compuesta, para cada
combinación de valores de verdad que se pueda asignar a sus componentes.
También es uno de los métodos más
sencillos y conocidos de la lógica formal, pero la mismo tiempo también uno de
los más poderosos y claros. Entender bien las tablas de verdad es, en gran
medida, entender bien a la lógica formal misma.
|
P
|
Q
|
^Q
|
|
1
|
1
|
1
|
|
1
|
0
|
0
|
|
0
|
1
|
0
|
|
0
|
0
|
0
|
Tablas de verdad trivalentes
Disyunción
Las tablas de verdad tradicionales pueden rescribirse si se
dejan vacías casillas en las que el valor de verdad de la fórmula atómica es
irrelevante, por ejemplo, la tabla de la disyunción:
Las primeras dos líneas señalan que no importa cuál sea el
valor de verdad de uno de los disyuntos, siempre que el otro sea verdadero, la
disyunción será verdadera. De la misma manera, se podría abreviar la tabla de
la conjunción de la siguiente manera:
Conjunción
Las últimas dos líneas señalan que no importa cuál sea el
valor de verdad de uno de los disyuntos, siempre que el otro sea falso, la
conjunción será falsa. La ventaja de este tipo de tablas es que permiten
extenderse de manera muy natural para permitir un tercer valor de verdad que no
sea ni verdadera ni falso. Será llamado “I” por “indeterminado”. Ahora se puede
usar la tabla abreviada de la disyunción clásica para desarrollar una tabla de
verdad (no abreviada) para la disyunción trivalente. Primer paso: identificar
las diferentes nueve posibilidades de combinaciones para dos variables
Disyunción trivalente
Segundo paso: Usar las primeras dos líneas de la tabla
abreviada para determinar el valor de verdad de los renglones con por lo menos
un argumento verdadero:
Conjunción trivalente
Tercer paso: Cómo la última línea de la tabla abreviada es
también la última línea de la nueva tabla, le corresponde el mismo valor de
verdad: falso.
Disyunción trivalente
Cuarto paso: Finalmente, cómo ya están los renglones que son
verdaderos o falsos según la tabla original, los renglones que aún no tienen
valor de verdad, dado que no son ni verdaderos (sino hubieran quedado como
tales en el segundo paso) ni falsos (ya que tampoco quedaron así en el tercer
paso), deben ser indeterminados!
En algunos casos, esta tabla de verdad aparece, no en tres
columnas, sino en un cuadro. Lo cual tiene la ventaja de dejar más claro el
patrón que emerge de la tabla. Siguiendo los mismos pasos se obtiene la tabla
de la conjunción:
Construcción de Tablas de Verdad
Algoritmo para construir una tabla de verdad de una fórmula
en lógica de proposiciones.
- Escribir
la fórmula con un número arriba de cada operador que indique su
jerarquía. Se escriben los enteros positivos en orden, donde el número 1
corresponde al operador de mayor jerarquía. Cuando dos operadores tengan
la misma jerarquía, se le asigna el número menor al de la izquierda.
- Construir
el árbol sintáctico
empezando con la fórmula en la raíz y
utilizando en cada caso el operador de menor jerarquía. O sea, del número
mayor al menor.
- Numerar
las ramas del árbol en forma secuencial empezando por las hojas hacia la
raíz, con la única condición de que una rama se puede numerar hasta que
estén numerados los hijos. Para empezar con la numeración de las hojas es
buena idea hacerlo en orden alfabético, así todos obtienen los renglones
de la tabla en el mismo orden para poder comparar resultados.
- Escribir
los encabezados de la tabla las fórmulas siguiendo la numeración que se le
dió a las ramas en el árbol sintáctico.
- Asignarle
a los átomos, las hojas del árbol, todos los posibles valores de verdad de
acuerdo al orden establecido. Por supuesto que el orden es arbitrario,
pero como el número de permutaciones es n!, conviene establecer un orden
para poder comparar resultados fácilmente.
- Asignar
valor de verdad a cada una de las columnas restantes de acuerdo al
operador indicado en el árbol sintáctico utilizando la tabla de verdad.
Conviene aprenderse de memoria las tablas de los operadores, al principio
pueden tener un resumen con todas las tablas mientras se memorizan.
- La
última columna, correspondiente a la fórmula original, es la que indica
los valores de verdad posibles de la fórmula para cada caso.

Lógica proporcional
Es una ciencia que estudia el lenguaje científico, su planteamiento, su organización, en entidades jerárquicas y los métodos como sus fórmulas para analizar toda forma escrita. Para comunicarse el ser humano utiliza lenguajes discursivos dichos lenguajes están llenos de partículas lógicas.
Es una rama de la lógica clásica que estudia las variables proposicionales o sentencias lógicas, sus posibles implicaciones, evaluaciones de verdad y en algunos casos su nivel absoluto de verdad.
Proposiciones

Tautología: se define tautología o validez a aquella formula que siempre es verdadera.
Contradicción: es una proposición que siempre es falsa para todos los valores de verdad. Para cualquier valor de verdad de las proposiciones, sea cual sea el resultado de la formula lógica estudiada siempre va a ser falso.
Conjunción: es aquella formula que es falsa o verdadera. Las expresiones de las que depende la validez de los argumentos se definen constante lógicas.
Conectores
Negación: no -> >, ~
Es una operación sobre proposiciones, valores de verdad, o en general, valores semánticos. Intuitivamente, la negación de una proposición es verdadera cuando dicha proposición es falsa, y viceversa.
Conjunción: Y ∧, Solamente si las componentes de la conjunción son ciertas, la conjunción es cierta.
Disyunción: O ∨,
La disyunción solamente es falsa si lo son sus dos componentes.
Condicional: ⇒ entonces
Típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad falso sólo cuando la primera proposición es verdadera y la segunda falsa.
Bicondicional: ⇔ si solo sí.
El Bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones.
Proposiciones
Variables: En el lenguaje simbólico de la lógica de proposiciones, a los enunciados simples, atómicos o elementales son los que no pueden descomponerse en otros más simples. Se les llama variables, y se escriben con las letras minúsculas del final del abecedario: “p”, “q”, “r”, “s”… para los casos particulares, o con las letras en mayúscula del principio del alfabeto cuando son casos generales: “A”, “B”, “C”, “D”…
Además de las variables, la lógica proposicional tiene otros elementos en su alfabeto: las constantes lógicas y los símbolos auxiliares que forman los enunciados compuestos.
Algunas de las marcas léxicas del lenguaje natural, se traducen con uno de las cinco constantes lógicas siguientes:
¬ NEGACIÓN: No
٧ DISYUNCIÓN INCLUSIVA: o, o bien, tanto si… como si,
٨ CONJUNCIÓN: y, e, o ni (=y no)
→ CONDICIONAL: si…. entonces
↔ BICONDICIONAL: si y solo si

 Es una expresión lógica que resulta verdadera para cualquier interpretación; es decir, para cualquier asignación de valores de verdad.La construcción de una tabla de verdad es un método efectivo para determinar si una expresión cualquiera es una tautología o no.
Es una expresión lógica que resulta verdadera para cualquier interpretación; es decir, para cualquier asignación de valores de verdad.La construcción de una tabla de verdad es un método efectivo para determinar si una expresión cualquiera es una tautología o no.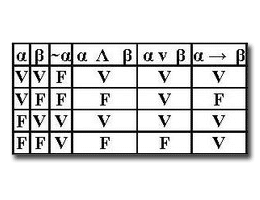
 Es la disciplina que trata de métodos de razonamiento. En un nivel elemental, la lógica proporciona reglas y técnicas para determinar si es o no valido un argumento dado. El razonamiento lógico se emplea en matemáticas para demostrar teoremas; en ciencias de la computación para verificar si son o no correctos los programas; en las ciencias física y naturales, para sacar conclusiones de experimentos; y en las ciencias sociales y en la vida cotidiana, para resolver una multitud de problemas. Ciertamente se usa en forma constante el razonamiento lógico para realizar cualquier actividad.En la filosofía para determinar si un razonamiento es válido o no, ya que una frase puede tener diferentes interpretaciones, sin embargo la lógica permite saber el significado correcto. En las matemáticas para demostrar teoremas e inferir resultados matemáticas que puedan ser aplicados en investigaciones.
Es la disciplina que trata de métodos de razonamiento. En un nivel elemental, la lógica proporciona reglas y técnicas para determinar si es o no valido un argumento dado. El razonamiento lógico se emplea en matemáticas para demostrar teoremas; en ciencias de la computación para verificar si son o no correctos los programas; en las ciencias física y naturales, para sacar conclusiones de experimentos; y en las ciencias sociales y en la vida cotidiana, para resolver una multitud de problemas. Ciertamente se usa en forma constante el razonamiento lógico para realizar cualquier actividad.En la filosofía para determinar si un razonamiento es válido o no, ya que una frase puede tener diferentes interpretaciones, sin embargo la lógica permite saber el significado correcto. En las matemáticas para demostrar teoremas e inferir resultados matemáticas que puedan ser aplicados en investigaciones.






