Tautologia y temas parecidos

Tautologia:

Es una expresión lógica que resulta verdadera para cualquier interpretación; es decir, para cualquier asignación de valores de verdad.La construcción de una tabla de verdad es un método efectivo para determinar si una expresión cualquiera es una tautología o no.

Es habitual que las tautologías sean consideradas como un error en el lenguaje o una falta de estilo. Sin embargo, es posible apelar a las tautologías para enfatizar una cierta idea. Por ejemplo: la oración “Puedo confirmar que el acusado es culpable ya que vi el asesinato con mis propios ojos”presenta una aclaración innecesaria acerca del uso de sus ojos, dado que no podría haber visto por otro medio; del mismo modo, el énfasis de la palabra “propios” puede omitirse absolutamente.

Tabla de verdad

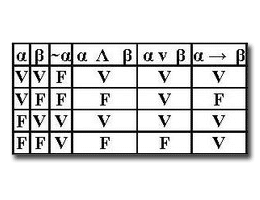
Presenta una proposición compuesta y su valor de verdad para cada una de las combinaciones posibles que se puedan dar con sus elementos. Su autor fue el filósofo y científico norteamericano Charles Sanders Peirce, también conocido como el máximo representante de la semiótica moderna, y la publicó a mediados de 1880.
Para configurar un sistema formal, es necesario establecer las definiciones de cada operador y los argumentos deben ser expuestos en forma de razonamientos deductivos lógico-lingüísticos, responder a un diseño puramente matemático y constituir una aplicación lógica que defina sus variables de entrada y salida.


Lógica matemática

Es la disciplina que trata de métodos de razonamiento. En un nivel elemental, la lógica proporciona reglas y técnicas para determinar si es o no valido un argumento dado. El razonamiento lógico se emplea en matemáticas para demostrar teoremas; en ciencias de la computación para verificar si son o no correctos los programas; en las ciencias física y naturales, para sacar conclusiones de experimentos; y en las ciencias sociales y en la vida cotidiana, para resolver una multitud de problemas. Ciertamente se usa en forma constante el razonamiento lógico para realizar cualquier actividad.En la filosofía para determinar si un razonamiento es válido o no, ya que una frase puede tener diferentes interpretaciones, sin embargo la lógica permite saber el significado correcto. En las matemáticas para demostrar teoremas e inferir resultados matemáticas que puedan ser aplicados en investigaciones.


Lógica Proporcional

Una lógica proposicional es un sistema lógico encargado de estudiar el razonamiento conforme a proposiciones.

Considera únicamente frases declarativas, las llamadas proposiciones o enunciados. A los que es posible asignar un valor de verdad o falsedad y ningún otro, es decir bivaluada (Principio del tercero excluido).

De este modo, su valor de verdad vendrá determinado por: el valor de verdad o falsedad de los enunciados simples que la componen, y las partículas no, o, y, si entonces, si y sólo si a modo de elementos de enlace.

Es libre de contexto. Esto es, la verdad o falsedad de los enunciados se establece sin recurrir a consideraciones de contexto alguno. Y sin considerar la estructura interna de los enunciados simples.